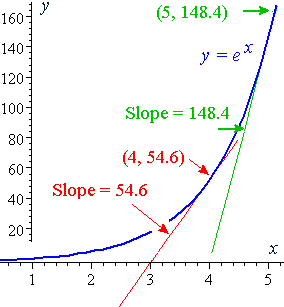
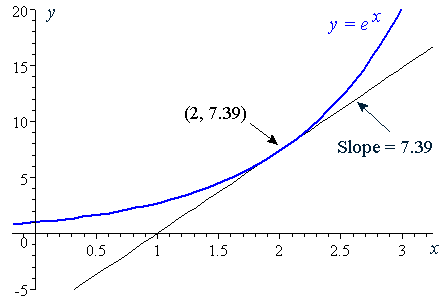
It means the slope is the same as the function value (the yvalue) for all points on the graph Example Let's take the example when x = 2 At this point, the yvalue is e 2 ≈ 739 Since the derivative of e x is e x, then the slope of the tangent line at x = 2 is also e 2 ≈ 739 We can see that it is true on the graphGraph y=e^ (x) y = e−x y = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0New Blank Graph Examples Lines Slope Intercept Form example Lines Point Slope Form example Lines Two Point Form example Parabolas Standard Form example Parabolas Vertex Form example Parabolas
Graphs Of Exponential And Logarithmic Functions Boundless Algebra
Y=e power x graph
Y=e power x graph-Experiment with the scales to find the crossover point The function ln x increases more slowly at infinity than any positive (fractionalUse "x" as the variable like this Examples sin(x) 2x−3;




Sketch The Region Bounded By The Curves And Find Its Area X E Y X E Y X Y 0 Study Com
However, graphs derived from realworld phenomena, like social networks and the web, typically have powerlawdegreedistributions,whichimpliesthatasmallsubset of the vertices connects to a large fraction of the graph Furthermore, powerlaw graphs are difficult to partition 1, 28 and represent in a distributed environment Homework Statement Consider the graph y = e^x Homework Equations Make an equation that results in reflecting about the line y = 2 The Attempt at a Solution I came up with 2 e^x And when I put it in my calculator it makes sense Just e^x is reflected among y = 0 so if youY=e^x y=e^x Log InorSign Up $$ ≥ $$ 1 $$ 2 $$ 3 $$ − A B C $$ $$ π $$ 0 $$ $$ = $$ Sign UporLog In to save your graphs!
Subject Column graph Inverse Scale Axis Y Hi @Vishesh Jain !Graph h ( x) = ( 1 / 3 ) –x I will compute the same points as previously Then the graph is So y = ( 1 / 3 ) –x does indeed model growth For the record, however, the base for exponential functions is usually greater than 1, so growth is usually in the form " 3 x " (that is, with a "positive" exponent) and decay is usually in the form " 3For what values of x is the graph of y=e^{x^{2}} concave down?
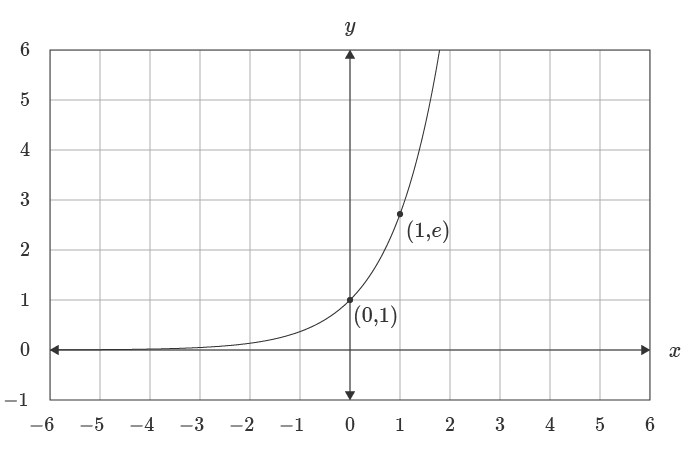
In this problem we have to use the chain rule y = e√x = ex1 2, convert the square root to its rational power The domain is RR, the range is (0;oo) The domain is the subset of RR for which all operations in the function's formula make sense Since e is a positive real constant, it can be raised to any real power, so the domain is not limited It is RR The range is the set of function's values Since a positive real constant is raised to a real power, the result is always positive, and is neverThe graph of y=2 x is shown to the right Here are some properties of the exponential function when the base is greater than 1 The graph passes through the point (0,1) The domain is all real numbers The range is y>0 The graph is increasing The graph is asymptotic to the xaxis as x approaches negative infinity



Content Graphing Logarithmic Functions




A X Y Y Ex X Belongs To R And B X Y Y E X X Belongs To R Then Write A Maths Meritnation Com
How To Given an exponential function with the form f(x) = bx c d, graph the translation Draw the horizontal asymptote y = d Shift the graph of f(x) = bx left c units if c is positive and right c units if c is negative Shift the graph of f(x) = bx up d units ifThus, the xaxis is a horizontal asymptoteThe equation = means that the slope of the For negative `x`values, the graph gets very close to the `x`axis, but doesn't touch it This is an exponential growth curve, where the yvalue increases and the slope of the curve increases as x increases Exponential Decay 5 10 15 10 30 40 50 60 70 80 90 100 t m(g) 65 Open image in a new page



How To Use The Excel Exp Function Exceljet




Art Of Problem Solving
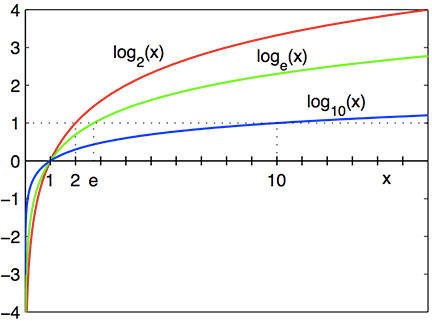
In particular, the area is \int_a^ {\ln (3)} (e^ {3x}8)\,dx where a is the value of x at which the curves y=e^ {3x} The plot corresponding to this question is so the area is not infinite In particular, the area is ∫ aln(3) (e3x −8)dx where a is the value of x at which the curves y = e3x What does it mean for an equation to beThe value of this series lies between 2 &3 it is represented by e Keeping e as base the function, we get y = e x, which is a very important function in mathematics known as a natural exponential function For a > 1, the logarithm of b to base a is x if a x = b Thus, log a b = x if a x = b This function is known as logarithmic functionThe x axis is an asymptote, the graph never crosses the x –axis When the base is greater than 1 And when the base is smaller than 1 Example To calculate the values of y , raise x to the power of the base y = 2 x Table of values Logarithmic functions An ordinary log function always has the points (1, 0) and (base, 1) since



Graphing Exponential Functions




Common Fixed Point Of A Power Graphic Contraction Pair In Partial Metric Spaces Endowed With A Graph Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free
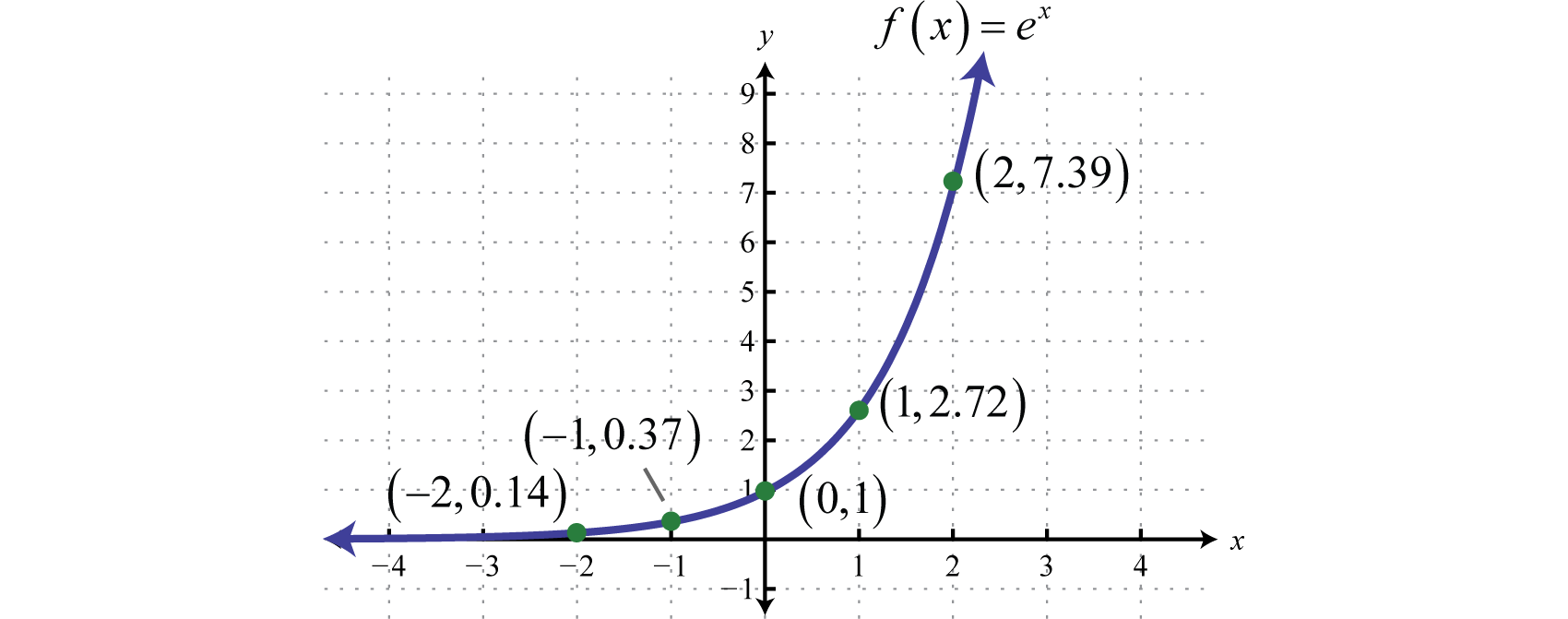
Definition 2 The exp function E(x) = ex is the inverse of the log function L(x) = lnx L E(x) = lnex = x, ∀x Properties • lnx is the inverse of ex ∀x > 0, E L = elnx = x • ∀x > 0, y = lnx ⇔ ey = x • graph(ex) is the reflection of graph(lnx) by line y = x • range(E) = domain(L) = (0,∞), domain(E) = range(L) = (−∞,∞)Summary f (x) = e x is the natural base exponential function 'e' is the natural base ' ≈ ' means 'approximately equal to' Plug each 'x' value into e x You can either use the 'e' button on your calculator or use the approximation 2718 for 'e' to find each value f (x) = e x has a horizontal asymptote along the xaxisVideo Transcript Okay, So once we separate the variables, we have the integral of why g to the power of winding Why is equal to the integral of axe times the square root of X squared plus one d x So for the left hand side and we can use the integration by parts to end up with eat the power of why multiplied by why minus one plus c one For the right hand side, we can use a substitution



Domain And Range Of Exponential And Logarithmic Functions




Solved 12 Find The Equation Of Tangent Line To The Graph Chegg Com
This might feel a bit more difficult to graph, because just about all of my yvalues will be decimal approximationsBut if I round off to a reasonable number of decimal places (one or two is generally fine for the purposes of graphing), then this graph will be fairly easyThis is because for 1 x tends to infinTherefore you to power minus X Squire four x squared 2 Should be less than zero And since if the power minus Squire Is always greater than zero for all X belongs to natural number, therefore we have Forex esquire 2 It's a blessing to zero on 40 square less than two or x
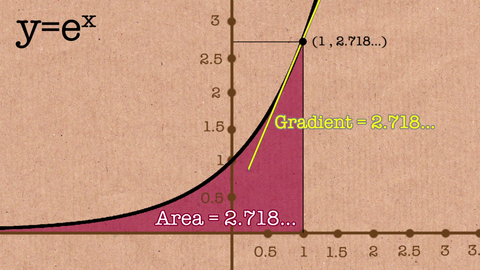



What S The Big Deal With Euler S Number Value Of E Constant




Graphs Of Exponential And Logarithmic Functions Boundless Algebra
0 Comments Show Hide 1 older comments Sign in to comment Sign inAbout Beyond simple math and grouping (like "(x2)(x4)"), there are some functions you can use as well Look below to see them all They are mostly standard functions written as you might expectThe exponential graph of a function represents the exponential function properties Let us consider the exponential function, y=2 x The graph of function y=2 x is shown below First, the property of the exponential function graph when the base is greater than 1 Exponential Function Graph for y=2 x The graph passes through the point (0,1)
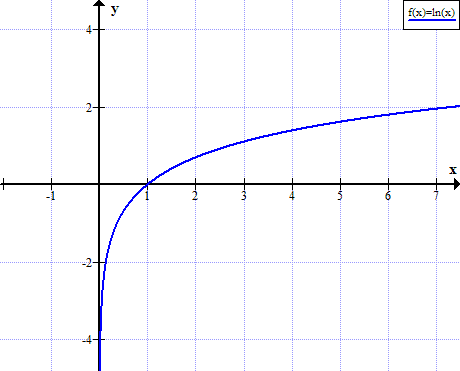



Natural Logarithm Rules Ln X Rules
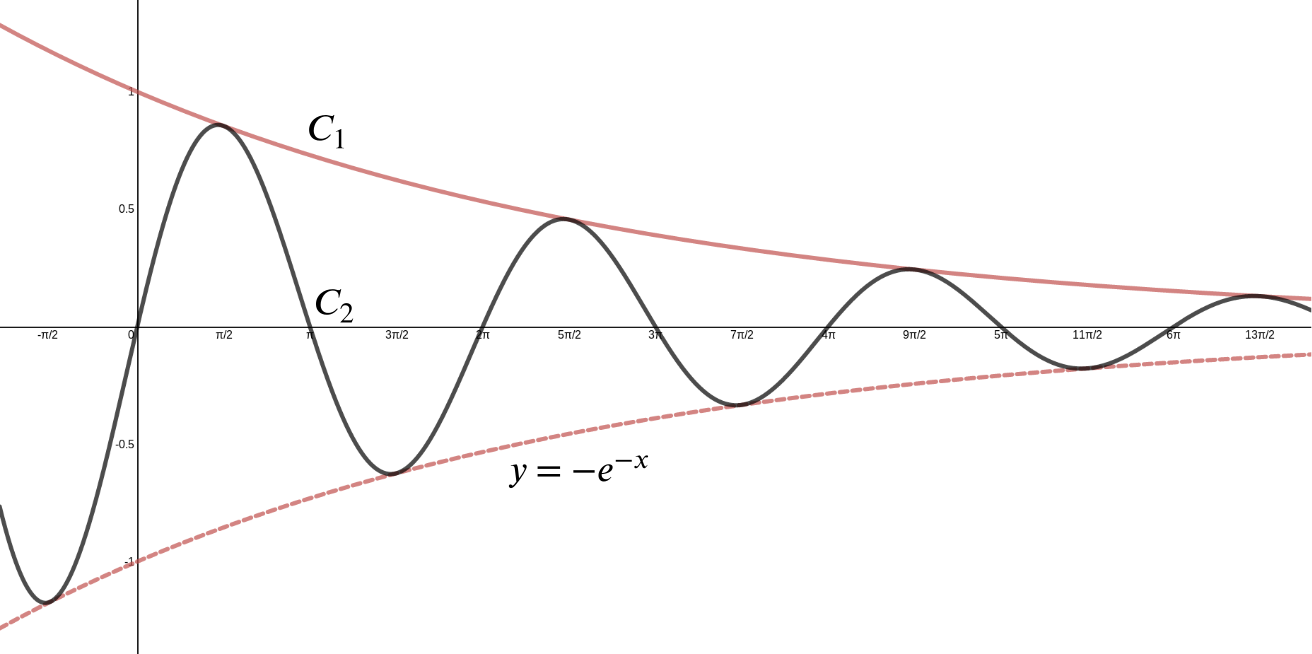



Solution Can We Find The Area Between Y E X And Y E X Sin X Product Rule Integration By Parts Underground Mathematics
2212 Graph the tenthdegree partial sum of y = 1/(1 x) in a 2, 2 x 2, 8 viewing window Use the " (" command to enter the partial sum Click here for the answer Investigating Another Power Series Consider the power series Graph the seventh, eleventh and fifteenthdegree polynomial partial sums in aMake the x scale big and the y scale huge!Exponential values, returned as a scalar, vector, matrix, or multidimensional array For real values of X in the interval (Inf, Inf), Y is in the interval (0,Inf)For complex values of X, Y is complex The data type of Y is the same as that of X



3 2 The Derivative As A Function Mathematics Libretexts



Graph Of E Power X
E x Calculator The Exp (x) function is used to determine e raised to the power of x If you want to solve e x =5, you need to take the natural log of both sides where e is the number also called as Napier's Number and its approximate value isOr is there another way to rewrite this equation?From the power series definition, it is clear that e t > 1 for t > 0 Take x > y and let t = x − y > 0 Then e x − y = e t > 1, which implies e x = e x − y e y > e y



What Is The Graph Of E X Quora
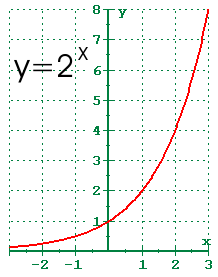



4 1 Exponential Functions And Their Graphs
So for any x value, you have a point on the curve, but you also have that point mirrored in the yaxis This means that for y=e^x you should draw y=e^x for then reflect that in the yaxis Another (and technically better) way to think about it is to consider the graphs separately, y=e^x when x is positive, and y=e^x when x is negative3 2 1 1 2 3 5 10 15 x y A graph of the exponential function y = ex It is important to note that as x becomes larger, the value of ex grows without bound We write this mathematically as ex → ∞ as x → ∞ This behaviour is known as exponentialgrowthThat will give you a table of x values (column A) and y values (column B) that you can plot on graph paper Your graph should look very much like Answer by josmiceli() ( Show Source )




Exponential Function Graph Algebra Video Khan Academy




Euler S Formula For Complex Numbers
Where a is a constant Figure 1 shows the graph of y=2^{x}, in blue, together with that of its gradient, in redNotice that the function itself and the gradient are very similar to one another they both rise rapidly as x gets larger Figure 1 graph of y=2^{x} (blue line) and its gradient (red line) Figure 2 shows y=3^{x} together with its gradient Again, the two curves are veryFrom the graphs, we find that for any nonzero real number b the domain of the exponential function y = e bx is the set of all real numbers, and the range is the set of all positive real numbers because the graph is above the xaxis The graph always passes through the point (0, 1)At the most basic level, an exponential function is a function in which the variable appears in the exponent The most basic exponential function is a function of the form y = bx y = b x where b b is a positive number When b > 1 b > 1 the function grows in



Exponential And Logarithmic Functions Logarithmic Functions Sparknotes



Function Definition Types Examples Facts Britannica
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsThe function ex decreases faster at infinity than any negative power Plot y = ex and y = x2 on the same axes Then plot y = ex and y = x on the same axes;Cos(x^2) (x−3)(x3) You can clickanddrag to move the graph around If you just clickandrelease (without moving), then the spot you clicked on will be the new center To reset the zoom to the original click on the Reset button raised to the power of a value or expression



Logarithmic And Exponential Graphs



What Is The Graph Of E X Quora
Graphing the function and the polynomial illustrate that the polynomial is a good approximation near x = 1 Graph y = e x and in a 2, 3, 1 x 3, 10, 1 window The secondorder Maclaurin polynomial you found in Lesson 242, , is tangent to f(x) = e x at x = 0 and has the same concavity as f(x) = e xGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Y=e^(x) is an exponential function which is decreasing in nature so it is monotonic Defining domain It takes all the real values as its input,from minus infinity to plus infinity This graph always remains above the Xaxis



6 Derivative Of The Exponential Function



Exponential Functions And Their Graphs
Unfortunately this way the view of the columns is cut only, but the position of crossing of the Xaxis in the Yaxis does not change (remains in 00) What I need is to "shift" the point at which the XThe former notation is commonly used for simpler exponents, while the latter is preferred when the exponent is a complicated expression The graph of = is upwardsloping, and increases faster as x increases The graph always lies above the xaxis, but becomes arbitrarily close to it for large negative x;Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history



Function And Relation Library
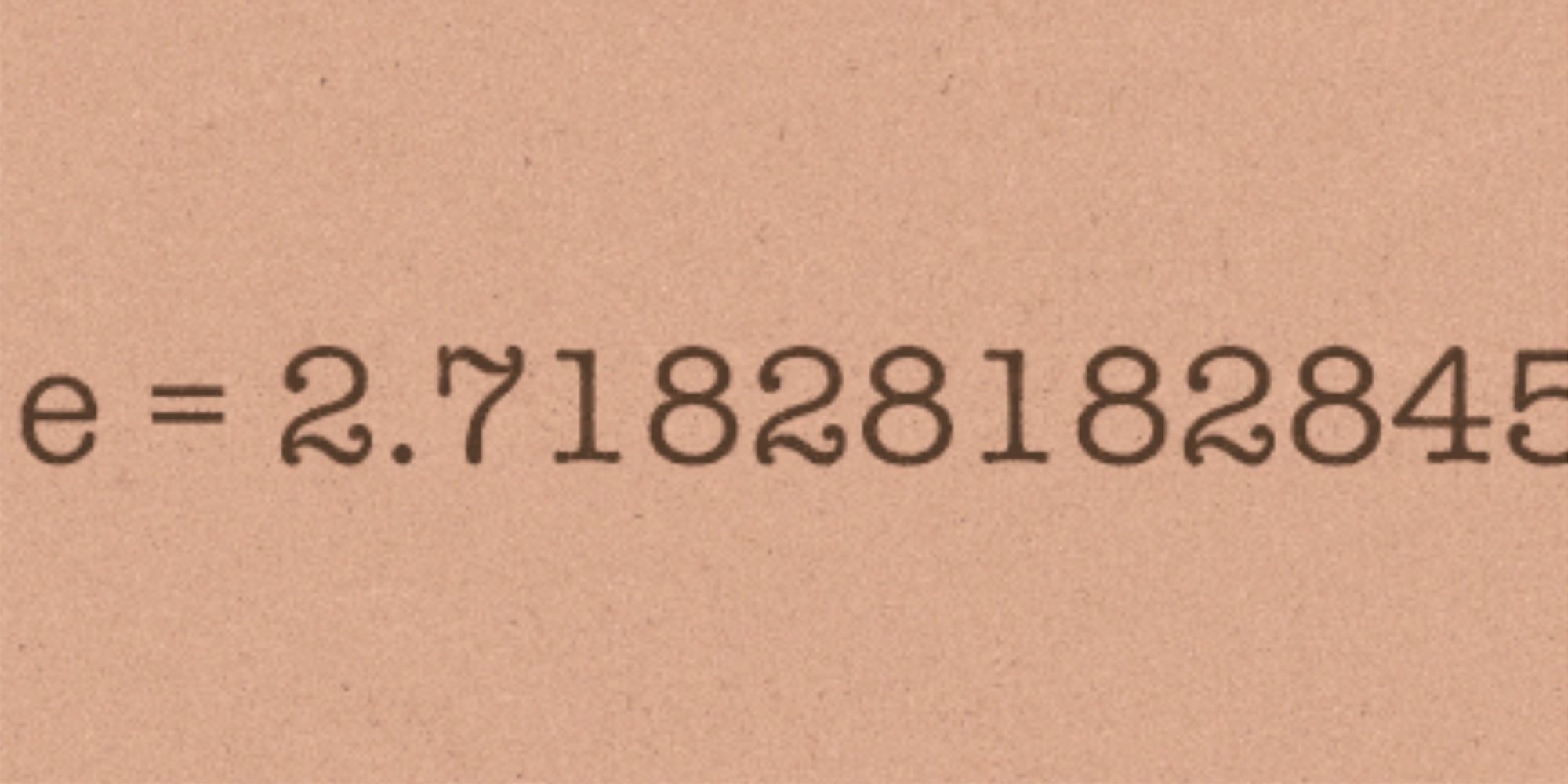



O Phnais Titnm
"Rational Solutions to x^y = y^x" CTK Wiki Math "x^y = y^x commuting powers" Arithmetical and Analytical Puzzles Torsten Sillke Archived from the original on dborkovitz () "Parametric Graph of x^y=y^x" GeoGebra OEIS sequence A (Decimal expansion of −x, where x is the negative solution to the equation 2^xE^x means that all the negative values of e^x will turn positive But, there is however a twist in this function, And that is, the graph of e^x is coincident to the graph of e^x Isn't it interesting!!!!The base 10 logarithm function Background Every positive number, y, can be expressed as 10 raised to some power, xThis relationship is described by the equation y = 10 x, and described by this graph For example the number 16 can be expressed as 10 12This is the black dot in the graph
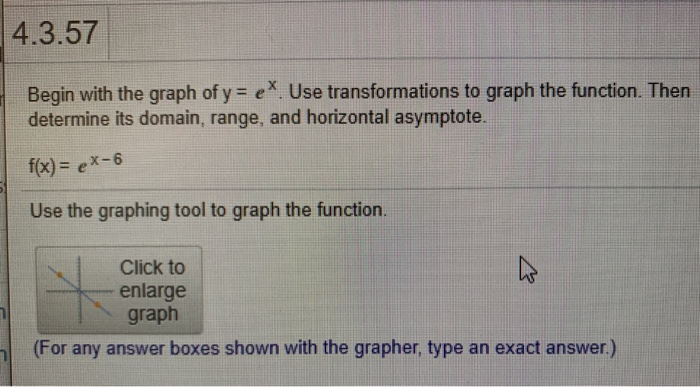



4 3 57 Please Guide Me Through How To Graph E To The Chegg Com




Working With Exponentials And Logarithms
Graph y = e x;Algebra Graph y=e^ (2x) y = e2x y = e 2 x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0Y = e x and y = ex In the more general form this appears as y = e ax and y = eax where a groups together any quantities that can be considered to be constant during the variation of x and y When graphed, these functions appear as seen in Figure 1 (note that when x = 0, y becomes = 1) Base e logarithms can be converted to base 10



Exponential Functions And Their Graphs



6 Derivative Of The Exponential Function
I have the task to plot a graph using the function y=e^x but I am having trouble with the constant e Do I have to define e first?Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
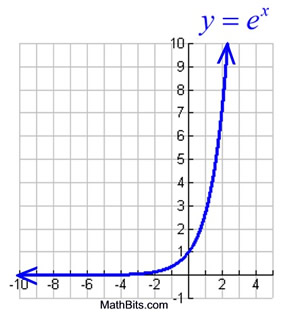



Natural Exponential Function And Natural Logarithmic Function Mathbitsnotebook Ccss Math
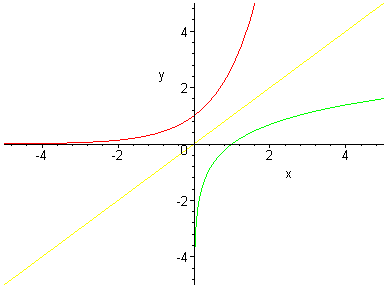



Exponentials And Logarithms Maths A Level Revision




Working With Exponentials And Logarithms




Prove 4 2 Using Infinite Exponents Can You Spot The Mistake Mind Your Decisions



Introduction To Exponential Functions



Privado Results




Differentiation Of The Exponential Function E X And Natural Logarithms Lnx Exponential Function E X Ppt Download



1




Calculus I Area Between Curves




Exponential Function Wikipedia



Content A Differential Equation For Exponential Growth And Decay




How To Find Equations For Exponential Functions Studypug



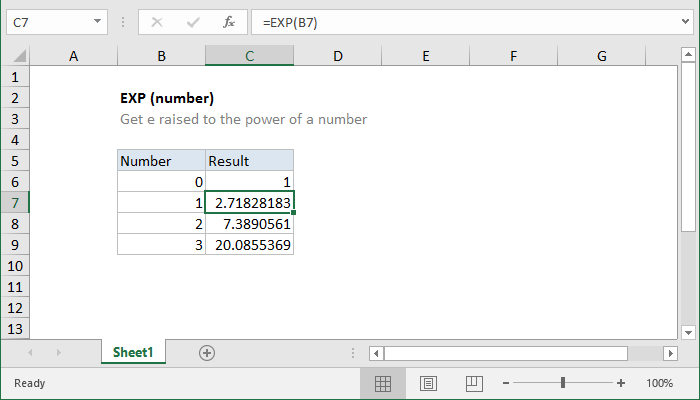
Exponential In Excel Formula Examples How To Use Exp Function



How To Use The Excel Exp Function Exceljet



How Can We Draw The Graph Of Y Log X E Base Is E Maths Doubts Goiit Com




A Graph Of Electric Field From 330kv At Mando Sub Station As A Download Scientific Diagram
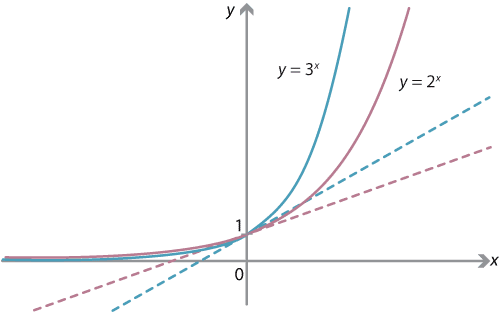



Content How Fast Does An Exponential Function Grow
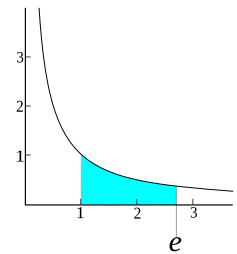



E Mathematical Constant Wikipedia
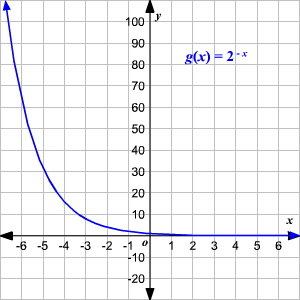



Domain And Range Of Exponential And Logarithmic Functions



2
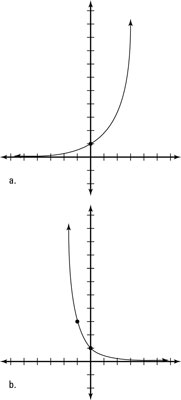



How To Graph And Transform An Exponential Function Dummies



6 Derivative Of The Exponential Function
/LinearRelationshipDefinition2-a62b18ef1633418da1127aa7608b87a2.png)



Linear Relationship Definition
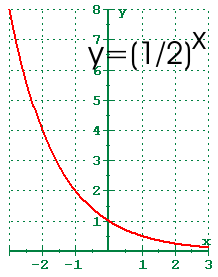



4 1 Exponential Functions And Their Graphs




Sketch The Region Bounded By The Curves And Find Its Area X E Y X E Y X Y 0 Study Com



Graph
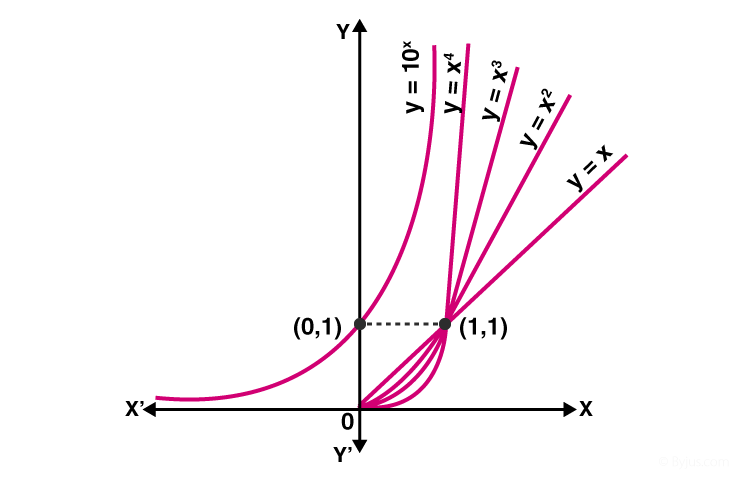



Exponential Functions Definition Formula Properties Rules




Exponential Graphs The Fizzics Organization
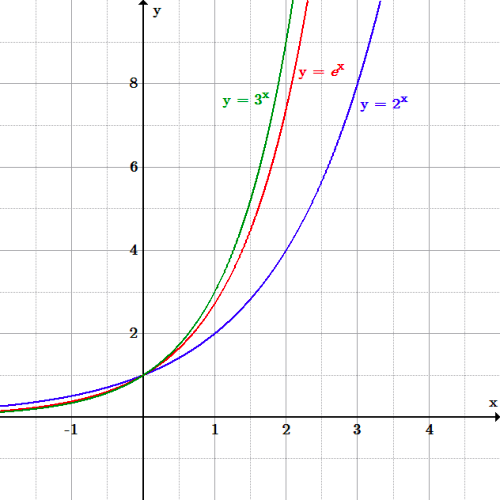



The Real Number E Boundless Algebra
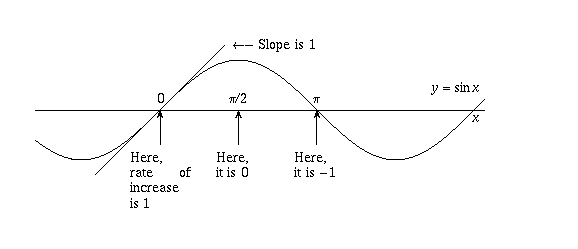



Question Corner Why Is E Pi I 1




Physics Mathematical Concepts Mathematical Principles Flashcards Quizlet
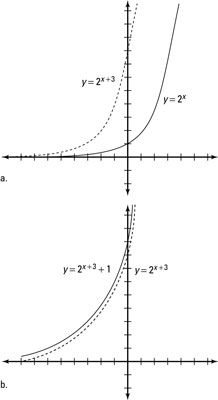



How To Graph And Transform An Exponential Function Dummies



Logarithmic And Exponential Graphs




Review
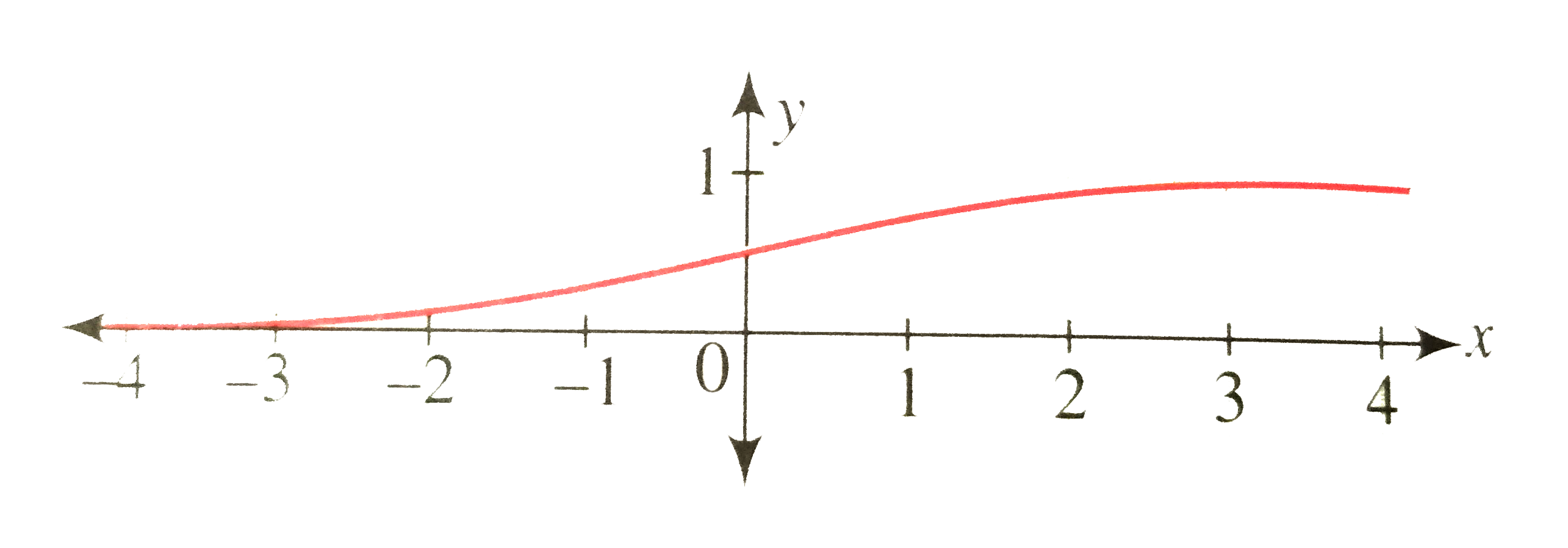



Draw The Graph Of F X E X 1 E X Also Find The Point Of
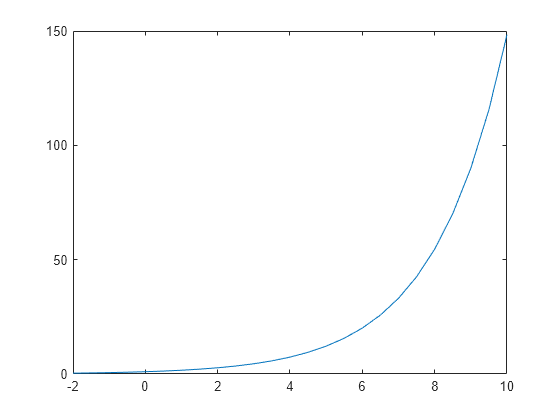



Exponential Matlab Exp
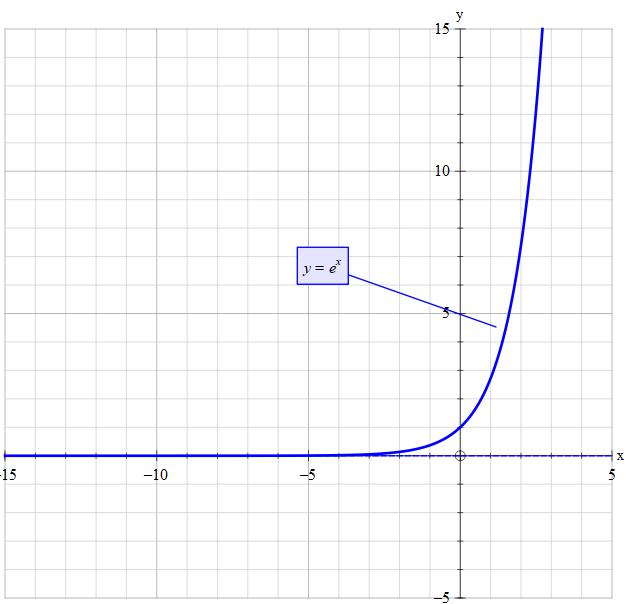



What Is The Domain And Range Of Y E X Socratic



3d Surface Plotter Academo Org Free Interactive Education
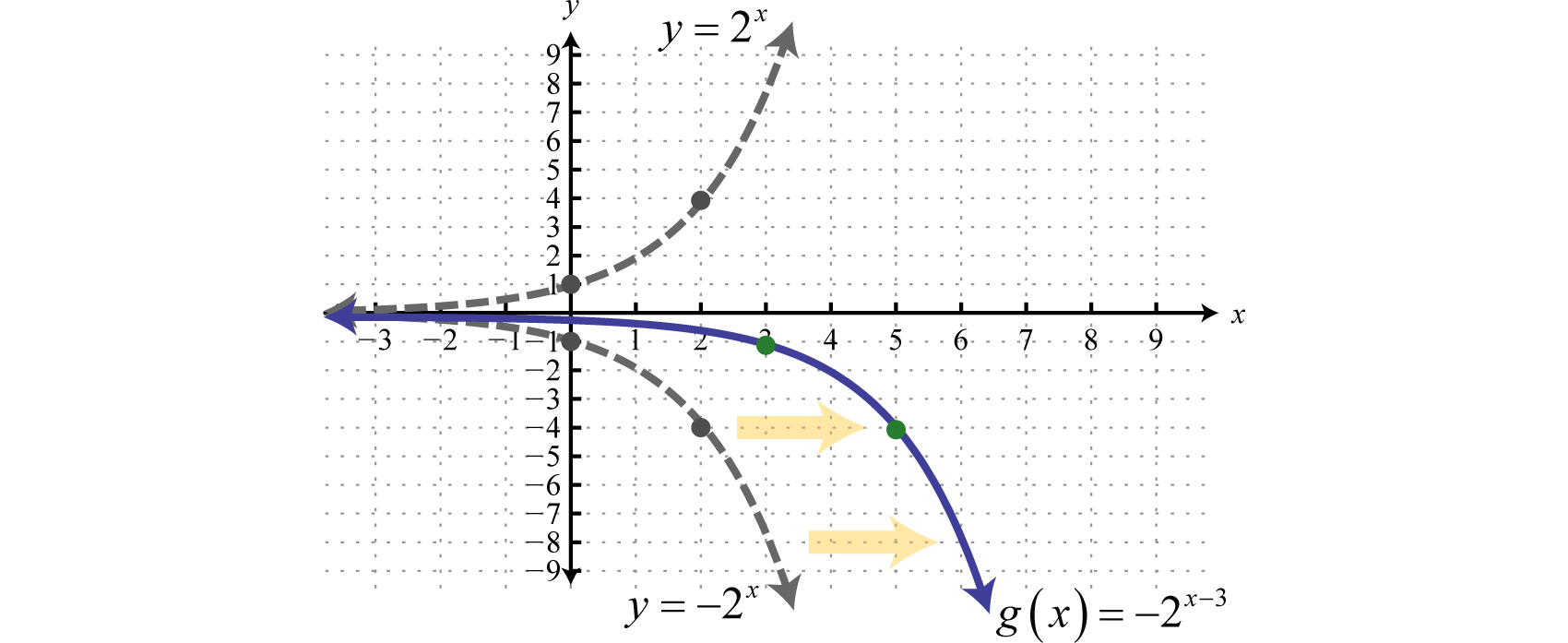



Exponential Functions And Their Graphs




3 6 Write The Expression As A Power Of E 3 4 4 Chegg Com




Differentiation Of The Exponential Function E X And Natural Logarithms Lnx Exponential Function E X Ppt Download



What Is The Graph Of E X Quora
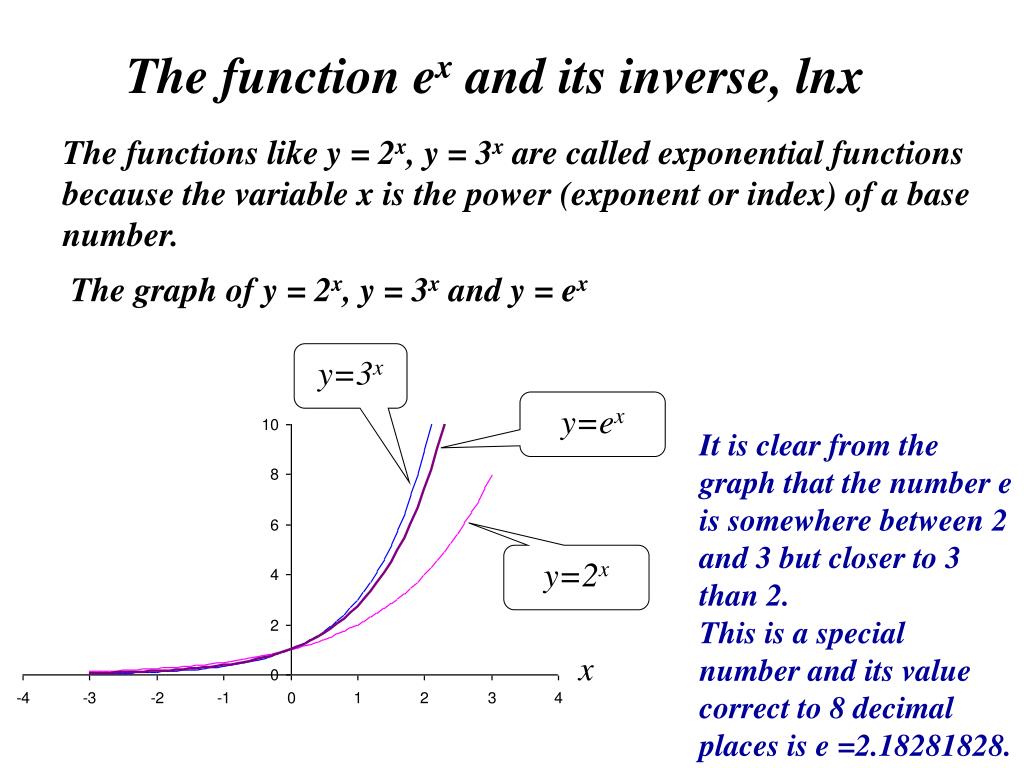



Ppt The Function E X And Its Inverse Lnx Powerpoint Presentation Free Download Id




Working With Exponentials And Logarithms
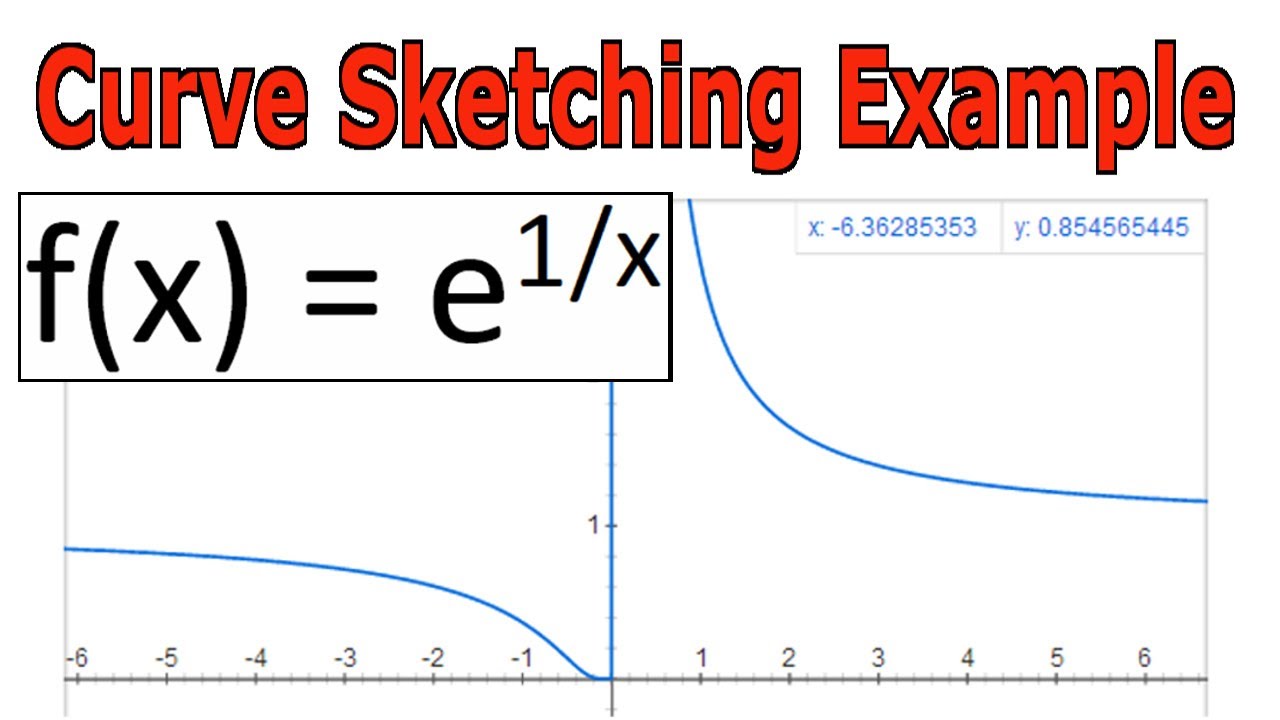



Curve Sketching Example Y E 1 X Youtube
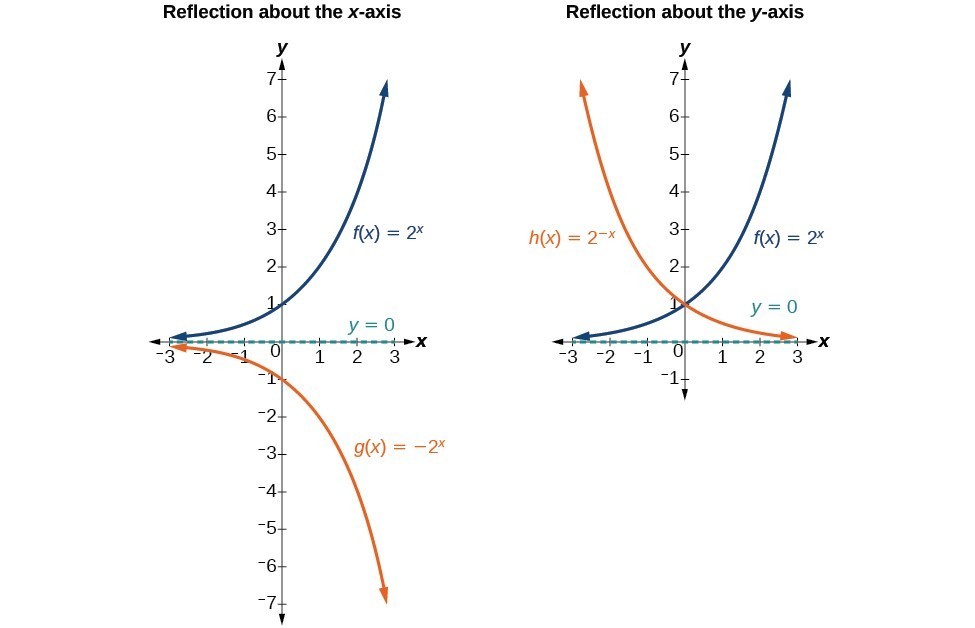



Stretching Compressing Or Reflecting An Exponential Function College Algebra



E X Formula
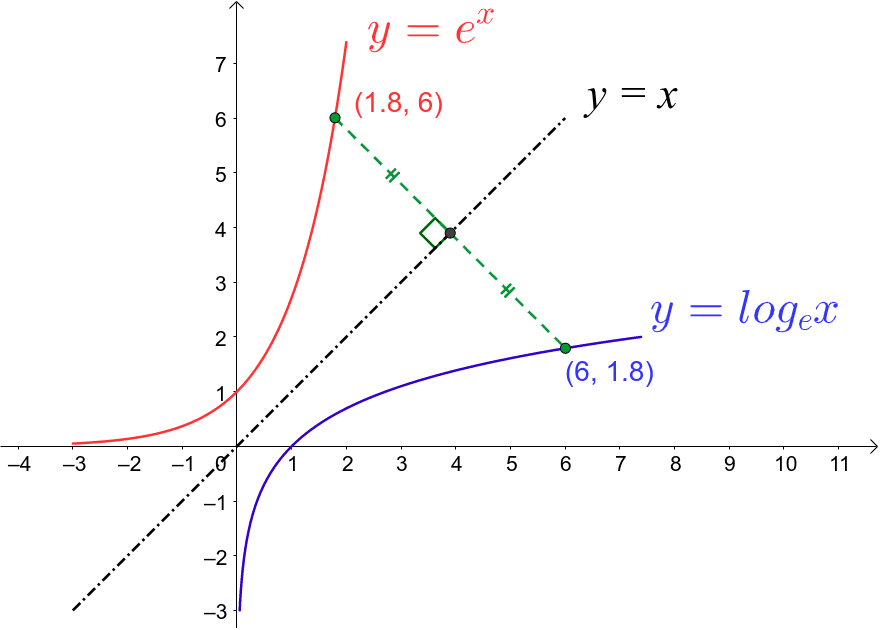



Graphs E X And Ln X Geogebra
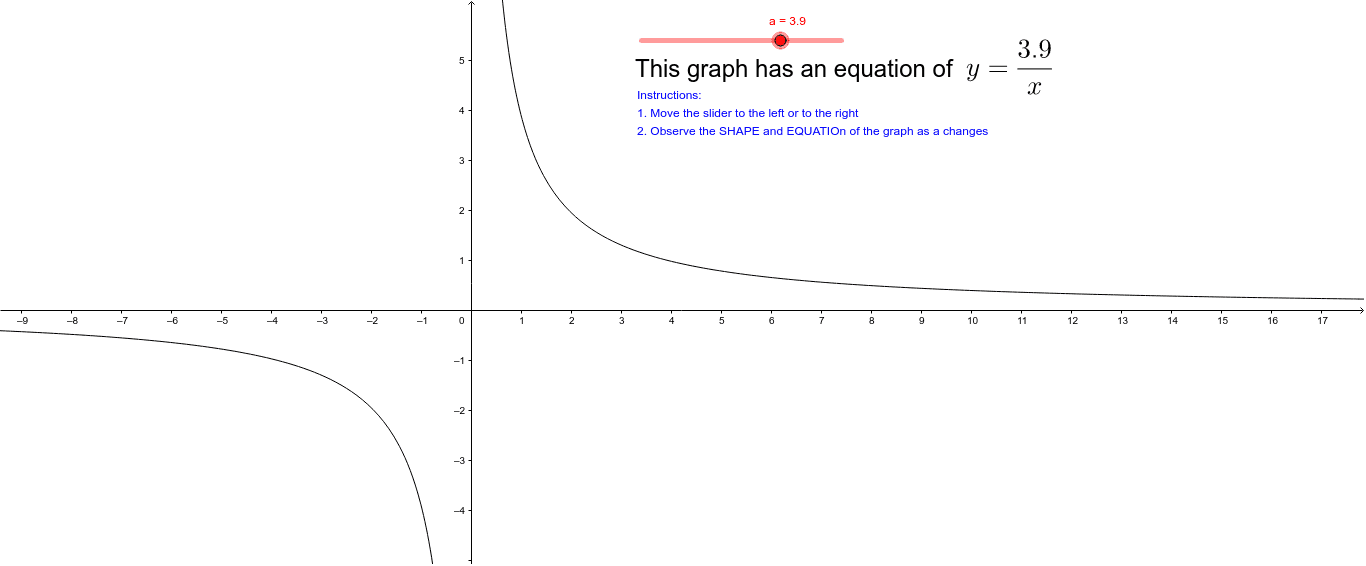



Power Function Graph Y A X Geogebra
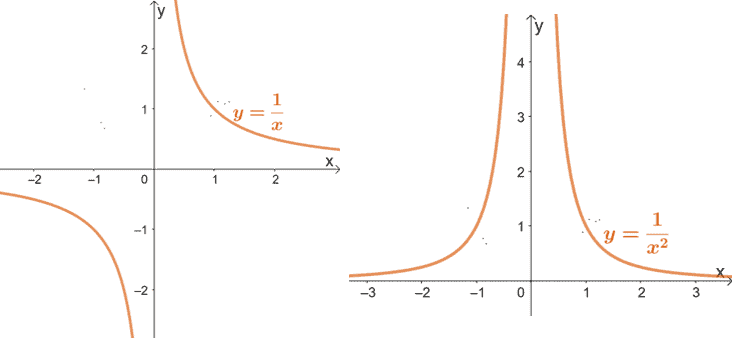



Power Function Properties Graphs Applications
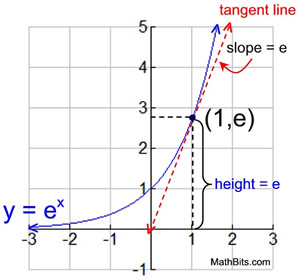



Natural Exponential Function And Natural Logarithmic Function Mathbitsnotebook Ccss Math
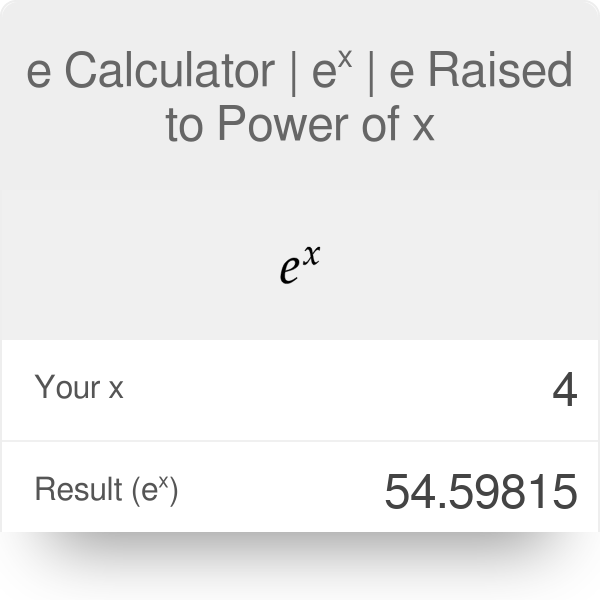



E Calculator Eˣ E Raised To Power Of X



2
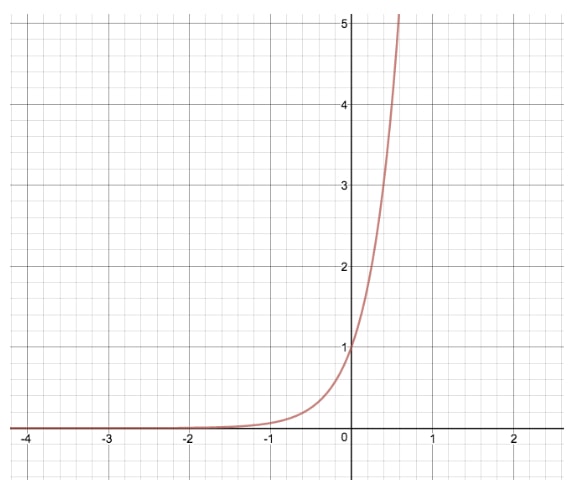



How To Find Equations For Exponential Functions Studypug




What Is An Exponential Function Video Lesson Transcript Study Com



What Is The Graph Of E X Quora



Logarithmic Functions Their Graphs
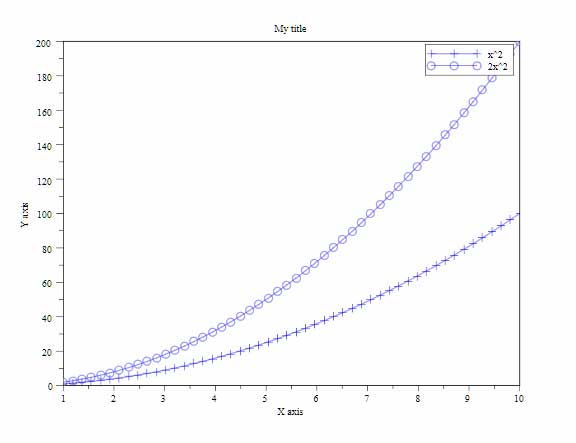



Plotting Www Scilab Org



2



Graphing The Natural Exponential Function Y E X Youtube



Graphing Exponential Functions Step By Step Instructions




Exponential Function Wikipedia




What Is The Graph Of E X Quora




Vertical Tangent To Curve X Y E Xy Mathematics Stack Exchange
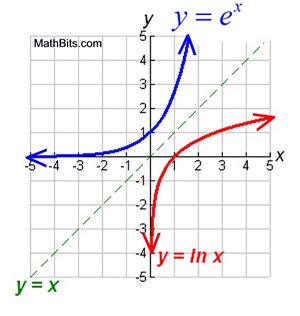



Natural Exponential Function And Natural Logarithmic Function Mathbitsnotebook Ccss Math




How To Differentiate Negative Exponentials
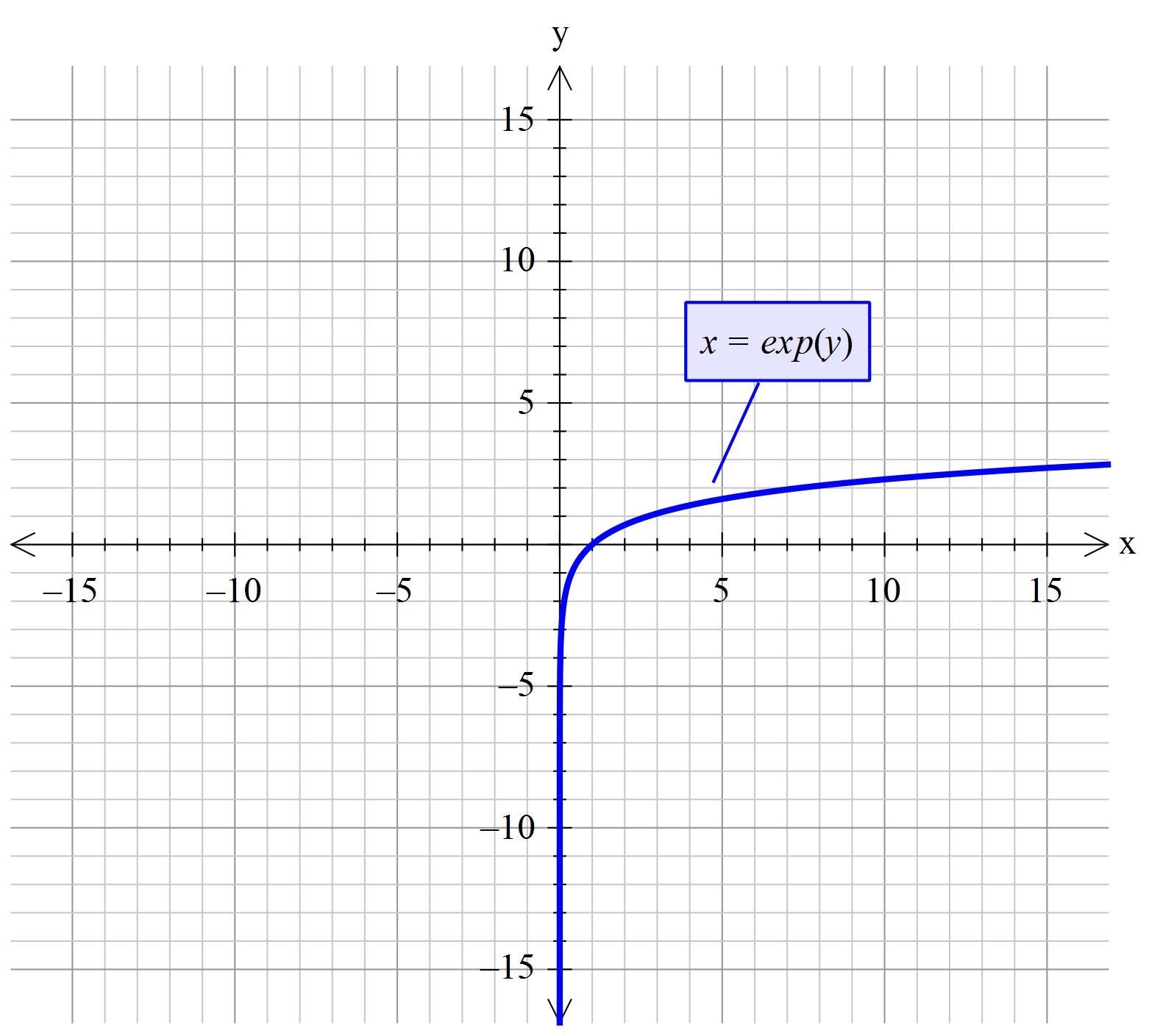



How Do You Graph X E Y Socratic



1




Question Regarding The Power Series For E X Mathematics Stack Exchange



Solution Can We Sketch And Describe These Composite Functions Combining Functions Underground Mathematics




Module 09 Natural Exponential Y E X



2



Y E Power X Graph




Derivative Of 𝑒ˣ Video Khan Academy



0 件のコメント:
コメントを投稿