Write a program to compute 1/22/33/4n/n1 with a given n input by console (n>0) Example If the following n is given as input to the program 5 Then, the output of the program should be 355 in Python by Dhineshbabu • 130 points •The sum of the first n squares, 1 2 2 2 n2 = n ( n 1) (2 n 1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula comes from Instead weView solution If a n 1 = a n − n 2 n and a 1 = 3 then the value of ∣ a 2 0 − a 1 5 ∣ =
2
1*2*3*4*5*n formula
1*2*3*4*5*n formula-To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234 Let term of the series 1 (1 2) (1 2 3) (1 2 3 4) (1 2 3 n) be denoted as an an = Σ n1 = = Sum of nterms of series Σ n1 a n = Σ n1 = Σ Σ = * * = Below is implementation of above approach




The Catalan Numbers And Their Applications 1 2
The hypothesis of Step 1) " The statement is true for n = k " is called the induction assumption, or the induction hypothesis It is what we assume when we prove a theorem by induction Example 1 Prove that the sum of the first n natural numbers is given by this formula 1 2 3 n = 3 Add a comment 6 According to Wikipedia S = n * (n 1) * (2*n 1) / 6 It is easy to prove this using induction Share edited Aug 1 '12 at 1745 For those of you who are unfamiliar with this series, which has come to be known as the Ramanujan Summation after a famous Indian mathematician named Srinivasa Ramanujan, it states that if you add all the natural numbers, that is 1, 2, 3, 4, and so on, all the way to infinity, you will find that it is equal to 1/12 Yup,
Find the sum ∑ r = 1 n r (r 1) 1 2 2 2 3 2 r 2 ?Making Equivalent Fractions 43 Rewrite the two fractions into equivalent fractions Two fractions are called equivalent if they have the same numeric value For example 1/2 and 2/4 are equivalent, y/ (y1)2 and (y2y)/ (y1)3 are equivalent as well To calculate equivalent fraction , multiply the Numerator of each fraction, by its We shall prove the result by principle of mathematical induction checking for n = 1, LHS 12 = 2 RHS 1/3 * 1 * 2 * 3 = 2 Hence true for n = 1
For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division! Find the sum up to n terms of the series 123 234 n(n1)(n2) In this 123 represent the first term and 234 represent the second term Examples Input 2 Output 30 123 234 = 6 24 = 30 Input 3 Output 90Solution Using the exponential formula (a m)(a n) = a mn where a = 4 4 3 $\times$ 4 2 = 4 32 = 4 5 = 1024



Cum Stabilesc O Formula Pentru Suma S 1 2 2 3 3 4 N N 1 Brainly Ro




A Sequence Is Shown Below 1 4 1 2 Select The Gauthmath
The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula = = () This equation was knownS n = 1 2 3 4 ⋯ n = k = 1 ∑ n k The elementary trick for solving this equation (which Gauss is supposed to have used as a child) is a rearrangement of the sum as follows S n = 1 2 3 ⋯ n S n = n n − 1 n − 2 ⋯ 1 \begin{aligned} S_n & = & 1 & & 2 & & 3 & \cdots & n \\ S_n & = & n & & n1 & & n2 & \cdots & 1 \\ \end{aligned} S n S n = = 1 n 2 n − 1 3 n − 2 ⋯ ⋯ n 1 Example 1 Find out the value of 5 2 – 3 2 Solution Using the formula a 2 – b 2 = (a – b)(a b) where a = 5 and b = 3 (a – b)(a b) = (5 – 3)(5 3) = 2 $\times$ 8 = 16 Example 2 4 3 $\times$ 4 2 = ?




Proof Using Induction Payment Proof



n Formula
(1) we will prove that the statement must be true for n = k 1 Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooExample Find the nth term of AP 1, 2, 3, 4, 5, a n, if the number of terms are 15 Solution Given, AP 1, 2, 3, 4, 5, a n n=15 By the formula we know, a n = a(n1)d Firstterm, a =1 Common difference, d=21 =1 Therefore, a n = 1(151)1 = 114 = 15




Pdf Important Sum Formulas Omid Motahed Academia Edu




1 2 2 3 3 4 N N 1 Formula Novocom Top
Homework Helper 3,798 94 Little ant said 1^2 2^2 3^2 2^n = 2^ (n1) This makes absolutely no sense I mean, look at it for a second firstly you failed to notice the pattern correctly since 2^n means 2^12^22^3 instead of what is shown And secondly, how can that all equal 2^ (n1) when on the left side of the equation, you(1 1/n) n (It gets more accurate the higher the value of n) That formula is a binomial, right?You know, it's not easy to answer the question without the proper context Second formula can also be used to find out number of combinations how to choose two elements out of n, or how many elements A i,j are in square matrix where i < j and probably one



Search Q 1 2b1 2 2b1 3 2b 2b1 N 3d Log N Tbm Isch



Search Q 1 2b2 2b3 2b 2bn Formula Tbm Isch
I am looking for a formula to which I can supply a number N and have it calculate 1234N I realise that I can enter 1 to N in as many cells then use SUM but this won't do for what I need to achieveDetermine if the Relation is a Function (1,2) , (2,3) , (3,4) , (4,5) , (5,6) Since there is one value of for every value of in , this relation is a function The relation is a functionAnswer to Let a_1=1 and then define a_{n1}=\\frac{7a_n}{n1} List the terms a_n and n=1,2,3,4,5 Write a formula for a_n =?




What Is The Sum Of The Series 1 2 2 3 3 4 4 5 N N 1 Quora




Formula 1 2 3 4
Simple and best practice solution for 4(3n1)=2(n3) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, soEach term is n 1, so 2S = (n 1) (n 1) (n 1) = n(n 1) Divide by 2 S = n(n 1) 2 My favourite proof is the one given here on MathOverflow I'm copying the picture here for easy reference, but full credit goes to Mariano SuárezAlvarez for this answer Please see below Induction method is used to prove a statement Most commonly, it is used to prove a statement, involving, say n where n represents the set of all natural numbers Induction method involves two steps, One, that the statement is true for n=1 and say n=2 Two, we assume that it is true for n=k and prove that if it is true for n=k, then it is also true for n=k1




Complete The Following Use Arithmetic To Evaluate Chegg Com




The Catalan Numbers And Their Applications 1 2
Can be used to divide mixed numbers 1 2/3 4 3/8 or can be used for write complex fractions ie 1/2 1/3 An asterisk * or × is the symbol for multiplication Plus is addition, minus sign is subtraction and () is mathematical parenthesesÎn cazul particular al primelor n numere naturale, suma 1 2 3 n este ușor calculabilă = = () Suma respectivă este numită și suma lui Gauss, fiind un caz particular al sumei termenilor unei progresii aritmetice cu rația 1 Vezi șiNow look at the small values of n f(1) = 1/2, f(2) = 1/2 1/6 = 2/3, f(3) = 2/3 1/12 = 3/4, f(4) = 3/4 1/ = 4/5, etc So for the first few small values of n, we have proven by demonstration that f(n) = n / (n1) Our task is to prove that if it works for any positive integer value of n, then it works for n 1 This way, it must by



2




Faulhaber S Formula Wikipedia
The Triangular Number Sequence is generated from a pattern of dots which form a triangle By adding another row of dots and counting all the dots we can find the next number of the sequence But it is easier to use this Rule x n = n (n1)/2 Example the 5th Triangular Number is x 5 = 5 (51)/2Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more Proving that123n is n (n1)/2 Here are four proofs One is very simple arithmetic, the second is nth Triangular number,123n is n (n1)/2 This is a visual one involving only the formula for the area of a rectangle This




Sequences And Arithmetic Sequences And Series




5 4 Mathematical Induction T
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history C Exercises Calculate the sum of the series (1*1) (2*2) (3*3) (4*4) (5*5) (n*n) Last update on (UTC/GMT 8 hours)1,2,3,4Tetrahydro2methylquinoline8carboxylic acid 1,2,3,4Tetrahydro2methylquinoline8carboxylic acid Synonyms 2Methyl1,2,3,4tetrahydroquinoline8carboxylic acid CAS Number




Section 8 4 Mathematical Induction Mathematical Induction In This Section We Are Going To Perform A Type Of Mathematical Proof Called Mathematical Induction Ppt Download




Use Principle Of Mathematical Induction It Can Be Proved 1 3 2 3 3 3 N 3 N N 1 2 2 For All N N
To prove the statement `1*22*33*4cdotsn(n1)=1/3n(n2)(n2)` we need to use induction First, let n=1 The left side is `1*2=2` The right side is `1/3 1(2)(3)=2` so the statement is true for n=1The number of possible high fives, H, within a group of n people is given by the formula h = 1/2(n^2n) After the Angels won the world seri Home / English / Mathematics / The number of possible high fives, H, within a group of n people is given by the formula h = 1/2(n^2n)As I know the formula for adding 1,2,3n is given by n (n1)/2 Comparing to above formula if we want to calculate sum up to n1 , using the above formula we get n1 (n11)/2 That is n (n1)/2 Thus the required formula is n (n1)/2 186K views




1 2 2 3 3 4 N N 1 Formula Novocom Top



Solved 1 A Show That The Difference Of The Squares Of Two Consecutive Triangular Numbers Is A Cube Can You Deduce From This A Formula For The Su Course Hero
We can also prove the given result using Mathematical Induction Let Sn = 123 234 345 n(n 1)(n 2) = n ∑ r=1r(r 1)(r 2) We want to prove that Sn = 1 4 n(n 1)(n 2)(n 3) ∀n ∈ N Let use consider the case n = 1 When n = 1 the given result gives LH S = S1About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsLHS = (1) (2) = 2 RHS = $$ \frac{(1)(11)(12)}{3} $$ Which is Equal to 2 Assume N = K $$ (1)(2) (2)(3) (3)(4) \cdots (k) (k1) = \frac{(k)(k1)(k2)}{3} $$ Proof that the equation is true for N = K 1 $$ (1)(2) (2)(3) (3)(4) \cdots (k) (k1) (k1) (k 2)$$ Which is Equal To $$ \frac{(k)(k1)(k2)}{3} (k1) (k 2)$$ This is where I've went so far
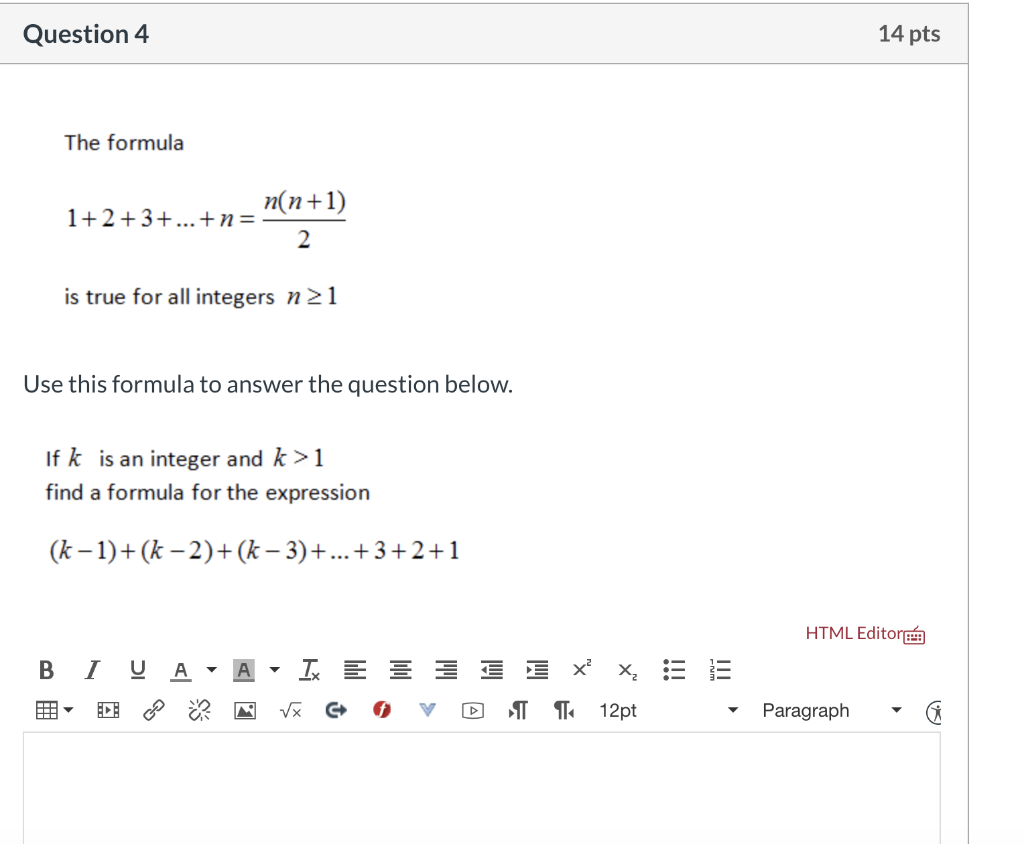



Question 4 14 Pts The Formula N N 1 1 2 3 N 2 Chegg Com




Prove By Mathematical Induction 3 4 5 N 2 N N Homeworklib
So let's use the Binomial Theorem First, we can drop 1 nk as it is always equal to 1 And, quite magically, most of what is left goes to 1 as n goes to infinity Which just leaves With just those first few terms we get e ≈ 270 Just double the regular formula To add evens from 2 to 50, find 1 2 3 4 25 and double it Sum of 2 4 6 n = 2 * (1 2 3 n/2) = 2 * n/2 * (n/2 1) / 2 = n/2 * (n/2 1) So, to get the evens from 2 to 50 you'd do 25 * (25 1) = 650 How about odd numbers, like 1 3 5 7 n?Solve for n (3/2)/ (1/4)=n 3 2 1 4 = n 3 2 1 4 = n Rewrite the equation as n = 3 2 1 4 n = 3 2 1 4 n = 3 2 1 4 n = 3 2 1 4 Simplify 3 2 1 4 3 2 1 4 Tap for more steps Multiply the numerator by the reciprocal of the denominator n = 3 2 ⋅ 4 n = 3 2 ⋅ 4 Cancel the common factor of 2 2




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter Geometric Progressions Download Free Pdf Available




Find The Sum Of N Terms Of The Series 1 2 4 1 4 6
Ex 41,2 Prove the following by using the principle of mathematical induction 13 23 33 n3 = ( ( 1)/2)^2 Let P (n) 13 23 33 43 n3 = ( ( 1)/2)^2In Exercises 115 use mathematical induction to establish the formula for n 1 1 12 22 32 n2 = n(n 1)(2n 1) 6 Proof For n = 1, the statement reduces to 12 = 1 2 3 6 and is obviously true Assuming the statement is true for n = k 12 22 32 k2 = k(k 1)(2k 1) 6; Best Answer #1 216 4 Assuming that the problem is 3 n 2 3 n 3 3 n 1 = 3 n ·3² 3 n ·3³ 3 n ·3 = 93 n 273 n 33 n = (9 27 3)3 n = 393 n



Http Www Manhassetschools Org Cms Lib8 Ny Centricity Domain 710 Hw 85 key 9h Pdf



How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora
K=n ∑k^k=1^12^23^3n^n (1) k=1 We can write as follows, k=n ∑k^k= 1^12^23^3(n1)^(n1)n^n (2) k=1 Subtract n^n on both sides k=n ∑k^kn^n = 1^12^23^3(n1)^(n1) (2) k=1 k=n1 ∑k^k(n^n)=x k=1 This is an arithmetic series, and the equation for the total number of times is (n 1)*n / 2 Example if the size of the list is N = 5, then you do 4 3 2 1 = 10 swaps and notice that 10 is the same as 4 * 5 / 2 Share I'd say, that if \frac{n(n1)}{2} is som of n numbers, then \frac{(n1)n}{2} is the sum of n1 numbers, do you agree?




Pdf Some Series Thomas Mcclure Academia Edu




Sum Of First 0 Natural Numbers
Find 3,5dialkoxyN4H1,2,4triazol4ylbenzamide and related products for scientific research at MilliporeSigma Add the two equations, term by term;



Http Fmwww Edu Gross Mt216 Hw04ans Pdf



Quiz 7 Notes



Is There Is Any Formula For 1 2 3 4 N And 1 2 2 2 3 2 N 2 Quora




Solved Use Iteration Guess Explicit Formula Please Solve Problem 2 Please Solve Using Arithmetic Q



Www Kent Ac Uk Smsas Personal Pf10 Ma304 Ex4 Sol Pdf




Sustainability Free Full Text Concreteness Fading Strategy A Promising And Sustainable Instructional Model In Mathematics Classrooms Html
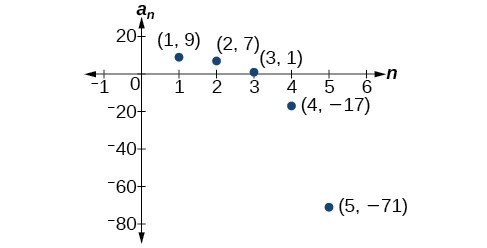



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Answered I Proving A Formula Use Mathematical Bartleby




Answered In Exercises 1 4 Use The Principle Of Bartleby
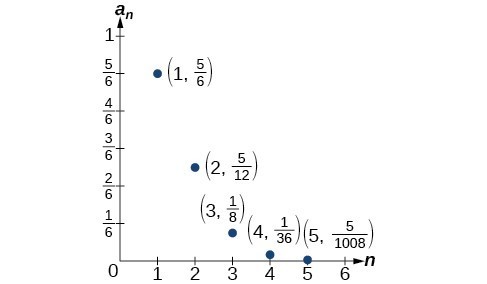



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange



1




Ex 4 1 6 1 2 2 3 3 4 N N 1 N N 1 N 2 3




1234n Formula




n Formula



2



2




Answered Double Check That The Maclaurin Series Bartleby
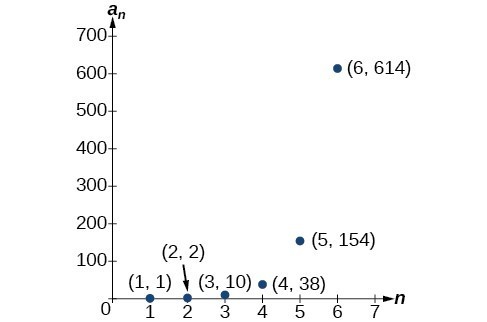



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




How To Sum 1 1 2 3 1 2 3 4 1 3 4 5 For Up To 10 Terms Quora




Answered Hello I Understand How To Do It That Bartleby




Math 6 Section 700 Experimentation Conjecture And Reasoning Spring 05




1234n Formula




1 Prove By Mathematical Induction 12 22 N2 Fra Gauthmath




Prove By Induction Sum Of The First N Cubes 1 3 2 3 3 3 N 3 Youtube



4 1 Higher Order Derivatives




How To 12 Proof By Induction 1 3 2 3 3 3 N 3 N N 1 2 2 N 2 N 1 2 4 Prove Mathgotserved Youtube



Jim Milner Sculpture Completing Alhazen S Formula




Prove 1 2 3 N N N 1 2 Mathematical Induction




Prep05sols Preparation For Tutorial Math1005 Answers To Question Set For B2 Sequences Page Of Throughout These Questions The Notation Will Be Used As Studocu



Http Www Kau Edu Sa Getfile Aspx Id Fn Assignments 2 mathematical induction1 Pdf




n2 Formula
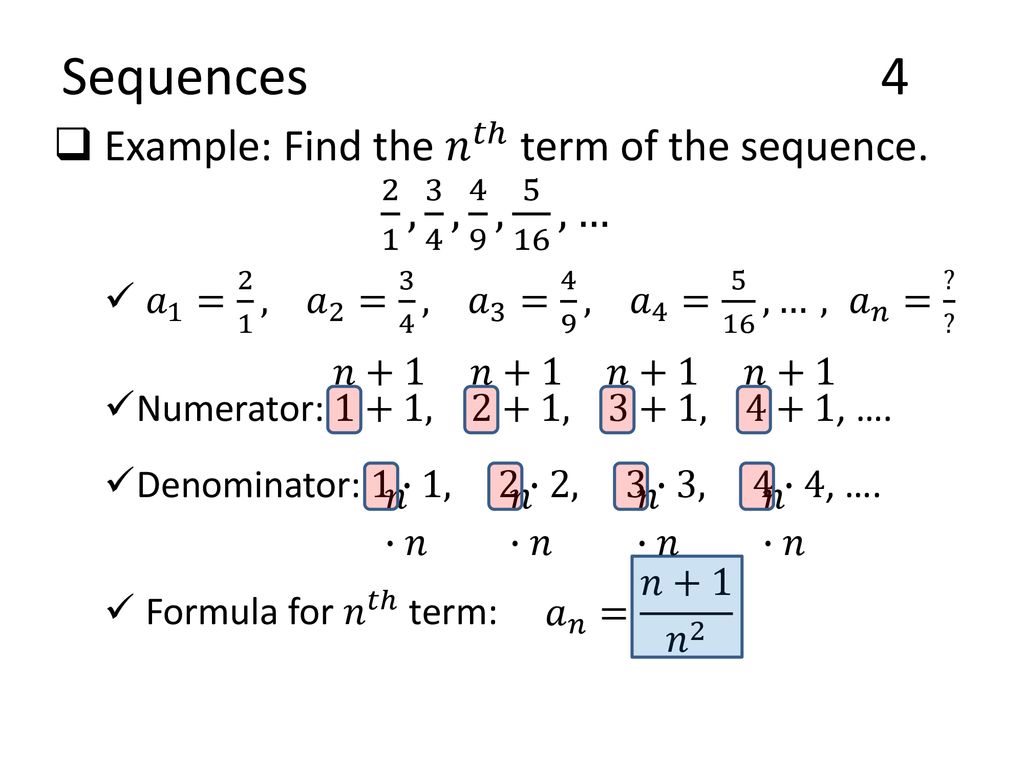



Sequences The Binomial Theorem Chapter Ppt Download



Python Challenges 1 Exercises Practice Solution W3resource




Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy



2



Find The Sum Of 4 1 N 4 2 N 4 3 N Up To The Nth Term Maths Areas Related To Circles Meritnation Com



Statmath Wu Ac At Hornik Comp Comp Exercises Pdf




Number Sequences Chapter 4 1 Of The Book




Solved 6 10 Points Integer N 2 1 Let P N Following Equation N 1 2 N2n 2 2 1 N 1 22 1 2 2 22 3 23 Q



Key Concepts In Computer Science Assignment 10 All Test Answers




Ex 4 1 6 1 2 2 3 3 4 N N 1 N N 1 N 2 3



2




Testing The Formula For F N Download Scientific Diagram




Use Mathematical Induction To Prove The Formula For Chegg Com




1 2 2 3 3 4 N N 1 Formula Novocom Top




Ramanujan S Sum Wikipedia



2




Special Series Definition Theorem Example Solution Mathematics
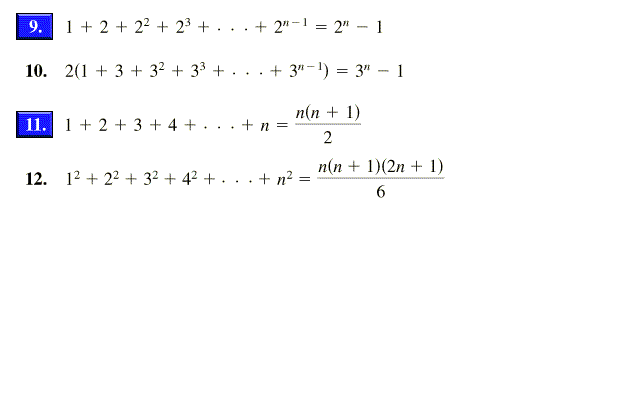



In Exercises 5 18 Use Mathematical Induction To Chegg Com




Use The Binomial Formula 1 Alpha N 1 N Alpha Chegg Com




Prove 1 2 3 N N N 1 2 Mathematical Induction




Formula For Sequence Of 0 0 1 1 2 2 3 3 4 4 And So On Non Geometric Non Arithmetic Mathematics Stack Exchange



Untitled Document



2




More On Sequences Some Sequences Are Not Arithmetic




How To Derive N 1 2 From 1 2 3 N N Quora
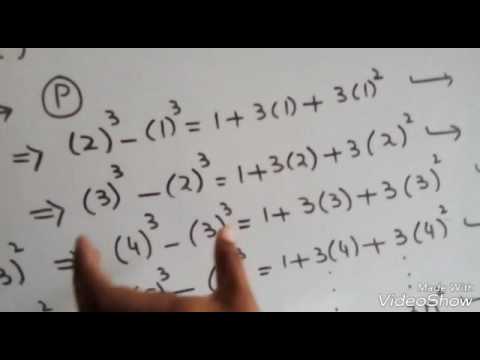



Prove That 1 2 2 2 3 2 N 2 N N 1 2n 1 6 Youtube
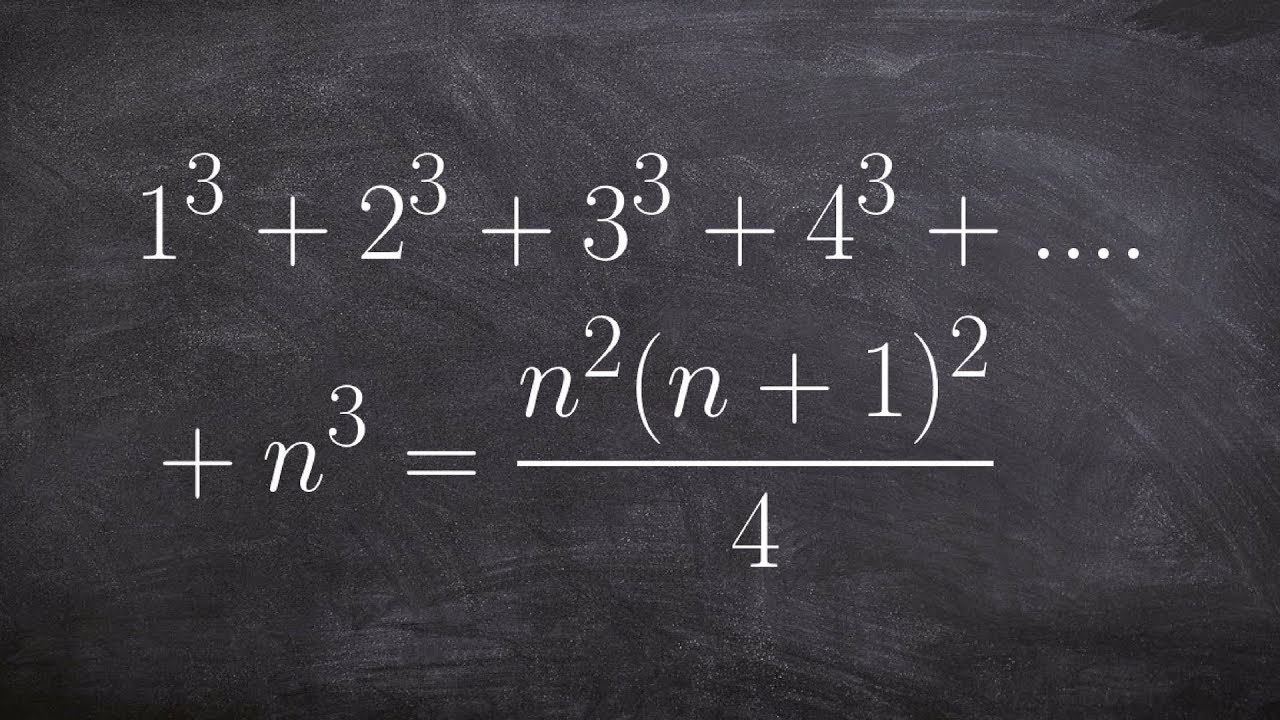



Learn To Use Induction To Prove That The Sum Formula Works For Every Term Youtube



2



2




1 2 2 3 3 4 N N 1 Formula Novocom Top




Gamma Function Wikipedia




Factorial Calculator Solve N Inch Calculator




Is This Modern Programming Interview Challenge S Solution Unreliable Stack Overflow




Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange




1 2 2 3 3 4 N N 1 Formula Novocom Top




More On Sequences Some Sequences Are Not Arithmetic




Squared Triangular Number Wikipedia



1



4 1 Higher Order Derivatives




1 2 2 3 3 4 N N 1 Formula Novocom Top



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




How To Proceed Further In This Arithmetico Geometric Progression Problem Mathematics Stack Exchange




Arithmetic Sequences And Series 1




Mathematics 103 Spring 00 Formulas For Simple Sequences



0 件のコメント:
コメントを投稿